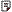连接AOC,OE和OB。
记x=BC=AB。记EB中点为F。由已知条件可得FB=x/3。
注意，（1）：∠FBO = ∠EBO （F没在图中标出），

在△OBC中，
（2）：tan(∠OCB)=r/x。
在△OFB中 （图中没画出），tan (∠FBO)=tan (∠EBO)，（公式 （1））。
由三角函数定义
（3）： tan (∠EBO)= \(\frac{\sqrt{r^2-(x/3)^2}}{(x/3)}\)

在△ABC中，
∠B=∠EBO+∠OBC=∠EBO+90°.另一方面
∠B=180°-2×∠OCB。即
（4）：∠EBO+90°=180°-2×∠OCB。

将（2），（3）代入（4）：
arctan (\(\frac{\sqrt{r^2-(x/3)^2}}{(x/3)}\)） +90°=180°-2× arctan (r/x)。

两边取正切（用三角公式）：
\(-\frac{x/3}{\sqrt{r^2-x^2/9}}=-\frac{2r/x}{1-r^2/x^2} \)
化简：
\(x^2-r^2=6r\sqrt{r^2-x^2/9}\)。
解之即得 \(x^2=5r^2\)

最后编辑时间: 2023-03-07 20:45:32