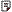��һ�⣺
���ķ����ܷ����ѳ����εĸ߷�Ϊ���Σ����·���ֱ�Ϊh��g��ͬ�����ѳ���Ϊ���Σ������ҷֱ���a��b��
���������Ϊx��
���������ο����������̣��ټ����Σ�
x+27+12=��2a+b����h+g��/2
�����������εķ��̿ɵ�24/a+54/(a+b)=30/b�����߳�b�ɵ�a/b=2��
����ɵã�h+g)=30/b��
�����������ι�ʽ����x=36��
�ڶ��⣺

�����Ҷ��������BD=sqrt(124)=11.13553��
�Ӷ��������Ҷ�����á�ADB: sin��ADB=5��(3)/��(124)��
����ACB=��ADB=51.05172��
�������Ҷ��� ���x��
x=2��(124) sin(B).
��B=��ABC������
B=180-30-��ACB��sin B=sin (30+��ACB)��������ֵ�⣺
sin B=0.9878292
x=22
���ķ����ܷ����ѳ����εĸ߷�Ϊ���Σ����·���ֱ�Ϊh��g��ͬ�����ѳ���Ϊ���Σ������ҷֱ���a��b��
���������Ϊx��
���������ο����������̣��ټ����Σ�
x+27+12=��2a+b����h+g��/2
�����������εķ��̿ɵ�24/a+54/(a+b)=30/b�����߳�b�ɵ�a/b=2��
����ɵã�h+g)=30/b��
�����������ι�ʽ����x=36��
�ڶ��⣺

�����Ҷ��������BD=sqrt(124)=11.13553��
�Ӷ��������Ҷ�����á�ADB: sin��ADB=5��(3)/��(124)��
����ACB=��ADB=51.05172��
�������Ҷ��� ���x��
x=2��(124) sin(B).
��B=��ABC������
B=180-30-��ACB��sin B=sin (30+��ACB)��������ֵ�⣺
sin B=0.9878292
x=22
���༭ʱ��: 2023-05-09 17:43:09