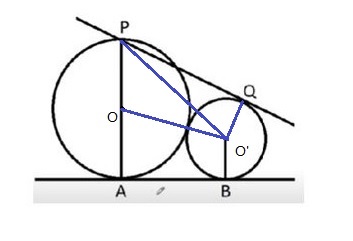
����Բ��Բ�ķֱ�Ϊ\(O��O'\) ����Բ�İ뾶�ֱ�Ϊ \(R��r\)�� \(2R = d\)��
����|\(AB| = L\)������Բ��֮��ľ���Ϊ \(R + r\)������ \[ ( R + r)^2 - L^2 = (R-r(^2\] �� \[ r= \frac{L^2}{4R}�� \]
��\(|PO'| = m\), \(|PQ|^2 = m^2 - r^2\)����֪ \[m^2 = L^2 + ( 2R - r)^2 ��\]���� \[m^2 - r^2 = L^2 + 4R^2 -4Rr = 4R^2 \]
��� \[ |PQ| = d.\]
���༭ʱ��: 2023-05-17 15:37:39


