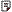不失一般性，令边长为2。以P为原点
记|MP|=d,即M的坐标为（-d,0)。

MO的斜率是√(3)/(3d)。
MO方程是√(3)x -3dy+√(3)d=0。
A坐标(-1,0)，B坐标(0,√(3))，C坐标(1，0）。
记A,B,C三顶点到该线距离为\(d_1,d_2,d_3\)

\(d_1=\frac{|\sqrt{3}d-\sqrt{3}|}{\sqrt{3+9d^2}}\)
\(d_2=\frac{|-3\sqrt{3}d-\sqrt{3}d|}{\sqrt{3+9d^2}}\)
\(d_3=\frac{\sqrt{3}(1+d)}{\sqrt{3+9d^2}}\)
继而
\(d_1^2=\frac{3(d-1)^2}{ 3+9d^2}\)
\(d_2^2=\frac{12d^2}{ 3+9d^2}\)
\(d_3^2=\frac{3(d+1)^2}{ 3+9d^2}\)
所以
\(d_1^2+d_2^2+d_3^2=\frac{18d^2+6}{ 3+9d^2}=2\)