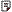不失一般性，设三角形边长为2。
以圆心为原点。三角形三个顶点坐标是：
A(-1, -1/√(3))，B(1,-1/√(3))，C(0,2/√(3))。

设圆周任一点坐标为(x,y)。该点到三顶点距离平方之和S为
\( S=(x+1)^2+(y+1/\sqrt{3})^2+(x-1)^2+(y+1/\sqrt{3})^2+x^2+(y-2/\sqrt{3})^2\)

化简可得\( S=3(x^2+y^2) +4\)，而圆半径平方=1/3，即\(x^2+y^2=1/3\)。

所以S=5。
如果三角形边长为a，则S=2.5a。

锟斤拷锟洁辑时锟斤拷: 2023-09-21 22:17:08